Resolução:
1ª Resolução:
Eu queria encontrar uma maneira melhor de resolver isso, sem ter que apelar pra geometria analítica. Queria achar uma solução por geometria plana mesmo, com semelhança e essas coisas. Mas por enquanto não achei nada melhor.
Coloque o vértice D no ponto zero dos eixos cartesianos, com os vértices A e C sobre os eixos y e x respectivamente. Chamemos de “a” o lado do quadrado, o que faz com que as coordenadas dos vértices sejam:
A(0, a), B(a, a), C(a, 0), D(0, 0)
Veja a figura:
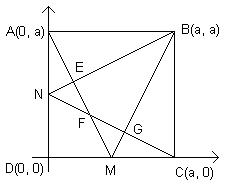
Como essa figura é simétrica, ao traçarmos BD, esse segmento passará pelo ponto F, e ainda dividirá o quadrilátero cuja área estamos procurando em dois triângulos congruentes. Então se acharmos a área do triângulo BEF, por exemplo, já teremos a área do quadrilátero procurada, que será o dobro da área desse triângulo.
A reta BD é a reta y = x e a reta AM é a reta y = -2x + a. E como F é o ponto de intersecção dessas duas retas:
x = -2x + a
3x = a
x = a/3
Então as coordenadas de F são (a/3, a/3). Agora podemos acahr as coordenadas do ponto E com a intersecção das retas BN e AM, cujas equações são respectivamente:
y = x/2 + a/2
y = -2x + a
E podemos achar as coordenadas do ponto E:
x/2 + a/2 = -2x + a
x + a = -4x + 2a
5x = a
x = a/5
y = -2x + a
y = -2.a/5 + a
y = -2a/5 + 5a/5
y = 3a/5
Assim, as coordenadas do ponto E são (a/5, 3a/5). E existe uma fórmula que nos dá a área de um triângulo se soubermos as coordenadas de seus vértices. Sejam os vértices do triângulo ABC os pontos A = (xA,yA), B = (xB,yB) e C = (xC,yC). Sua área é igual a:
= (1/2). |xA yA 1|
|xB yB 1|
|xC yC 1|
É igual a metade do módulo desse determinante. Entâo, como já temos as coordenadas dos pontos B, E e F, podemos descobrir a área do triangulo BEF usando essa fórmula.
= (1/2). |xB yB 1|
|xE yE 1|
|xF yF 1|
= (1/2). | a a 1|
|a/5 3a/5 1|
|a/3 a/3 1|
= (1/2).[3a2/5 + a2/3 + a2/15 – 3a2/15 – a2/3 – a2/5]
= (1/2).[3a2/5 + a2/15 – 3a2/15 – a2/5]
= (1/2).[2a2/5 – 2a2/15]
= (1/2).[6a2/15 – 2a2/15]
= (1/2).(4a2/15)
= 2a2/15
E como a área do quadrado era a2 que o problema chamou de S, a área do triângulo BEF é igual a 2S/15.
Como já vimos que o triângulo BGF (por simetria) tem a mesma área que o triângulo BEF, a área do quadrilátero BEFG é:
BEFG = BEF + BFG
BEFG = BEF + BEF
BEFG = 2.BEF
BEFG = 2.2S/15
BEFG = 4S/15
_____________________________________________________________
2ª Resolução:
Outra solução semelhante, usando os pontos médios dos lados AB e BC. Coloque o vértice D no ponto zero dos eixos cartesianos, com os vértices A e C sobre os eixos y e x respectivamente. Chamemos de “L” o lado do quadrado, o que faz com que as coordenadas dos vértices sejam:
A(0, L), B(L, L), C(L, 0), D(0, 0)
Veja a figura:
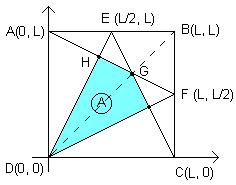
Nela você pode ver os pontos médios E e F com suas coordenadas (L/2, L) e (L, L/2) respectivamente. Como essa figura é simétrica, ao traçarmos BD, esse segmento passará pelo ponto G, e ainda dividirá o quadrilátero cuja área estamos procurando em dois triângulos congruentes. Então se acharmos a área do triângulo DGH, por exemplo, já teremos a área do quadrilátero procurada, que será o dobro da área desse triângulo.
A reta BD é a reta y = x (é a reta que passa pelos pontos (0, 0) e (L, L)) e a reta AF é a reta y = -x/2 + L (passa pelos pontos (0, L) e (L, L/2)). E como G é o ponto de intersecção dessas duas retas, temos que igualar o valor de y das duas equações:
x = -x/2 + L
3x/2 = L
x = 2L/3
Então as coordenadas de G são (2L/3, 2L/3).
Agora podemos achar as coordenadas do ponto H com a intersecção das retas AF e DE, cujas equações são respectivamente:
y = -x/2 + L
y = 2x
E podemos achar as coordenadas do ponto H se igualarmos os valores de y das duas equações:
-x/2 + L = 2x
L = 2x + x/2
5x/2 = L
x = 2L/5
Achamos a abcissa de H, agora achamos a ordenada:
y = 2x
y = 2.2L/5
y = 4L/5
Assim, as coordenadas do ponto H são (2L/5, 4L/5).
Agora vemos que se chamarmos a área que queremos de A, podemos escrever que:
A/2 = ABD – AGB – AHD
Onde ABD, AGB e AHD são as áreas desses 3 triângulos. A área de ABD é metade da área do quadrado ABCD que tem lado L e portanto área igual a L2.
Para acharmos a área de AGB, chamaremos de base do triângulo o lado AB, que tem medida L. Assim a altura do triângulo será a distância de AB até G. Como a distância de G até o lado CD, que é o eixo x, é de 2L/3 pois este é o valor da sua coordenada y, a distância de G até o lado AB será 1/3 porque a soma dessas duas distâncias tem que dar o tamanho da altura do quadrado, que é L. Agora achamos a área do triângulo de base L e altura L/3:
AGB = L.(L/3)/2
AGB = L2/6
Para o triângulo AHD, chamaremos de base o lado AD que tem medida L e nesse caso a altura do triângulo será a distância de H até o lado AD, que é o eixo y, e assim será exatamente o valor da coordenada x do ponto H, que é 2L/5. Agora acharemos a área do triângulo de base L e altura 2L/5:
AHD = L.(2L/5)/2
AHD = L2/5
E agora vamos achar o valor de A que é metade da área que temos ao tirar as áreas de AGB e AHD da área ABD:
A/2 = ABD – AGB – AHD
A/2 = L2/2 – L2/6 – L2/5
A/2 = (15L2 – 5L2 – 6L2)/30
A/2 = 4L2/30
A/2 = 2L2/15
A = 4L2/15
Mas o problema pediu a área em função da área S do quadrado. Assim, como sabemos que S = L2, podemos escrever que:
A = 4S/15
