Resolução:
Essa é complicada. Esbocei uma figura pra tentar facilitar.
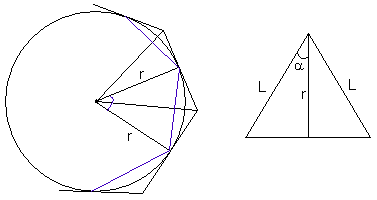
Primeiro vamos aos polígonos de n lados inscrito e circunscrito. Se você tem um polígono de n lados inscrito numa circunferência (na figura está em azul), você pode dividí-lo em n triângulos isósceles com dois lados iguais ao raio da circunferência. Assim, você pode calcular o ângulo entre esses lados, porque como você tem n triângulos, e a circunferência toda tem 2.pi radianos, esse ângulo entre os lados iguais dos triângulos são todos iguais a 2.pi/n, pois você dividiu a circunferência toda em n ângulos.
Agora você pode usar a fórmula da área do triângulo que usa dois lados e o seno entre eles para achar a área de um desses triângulos. Você tem dois lados iguais ao raio e o ângulo entre eles vale 2.pi/n:
= r.r.sen(2.pi/n)/2
= r2.sen(2.pi/n)/2
E você sabe que “s” é a soma de n vezes a área desse triângulo:
s = n.r2.sen(2.pi/n)/2
Agora façamos o mesmo para o polígono circunscrito. No caso desse polígono de n lados, só que circunscrito, ao dividí-lo em n triângulos, o ângulo entre os lados iguais também vale 2.pi/n, mas agora o lado não é mais r. Agora r é a altura desse triângulo. Veja o triângulo na figura acima. L é o lado do triângulo, r é a altura e o ângulo alfa (a) é metade do ângulo do triângulo entre os lados congruentes (2.pi/n), então a = pi/n.
Para acharmos o lado do triângulo em função do raio podemos usar o cosseno de a:
cos a = r/L
cos (pi/n) = r/L
L.cos (pi/n) = r
L = r/[cos (pi/n)]
Agora podemos achar a área de um desses triângulos com dois lados iguais a r/[cos (pi/n)] e o ângulo entre eles igual a 2.pi/n:
= {r/[cos (pi/n)]}.{r/[cos (pi/n)]}.sen (2.pi/n)/2
= r2.sen (2.pi/n)/2.[cos (pi/n)]2
E você sabe que “S” é a soma de n vezes a área desse triângulo:
S = n.r2.sen (2.pi/n)/2.[cos (pi/n)]2
Para melhorar um pouco a cara dessas fórmulas, vou fazer a = pi/n e 2a = 2.pi/n:
s = n.r2.sen(2.pi/n)/2
s = n.r2.sen(2a)/2
s = n.r2.2.(sen a).(cos a)/2
s = n.r2.(sen a).(cos a)
S = n.r2.sen (2.pi/n)/2.[cos (pi/n)]2
S = n.r2.sen (2a)/2.(cos a)2
S = n.r2.2.(sen a).(cos a)/2.(cos a)2
S = n.r2.(sen a).(cos a)/(cos a)2
S = n.r2.(sen a)/(cos a)
Até aí tudo bem. Agora vamos ver os polígonos de 2n lados. Eles são praticamente iguais a esses. Então para o polígono inscrito temos a mesma coisa que para o de n lados.
Se você tem um polígono de 2n lados inscrito numa circunferência, você pode dividí-lo em 2n triângulos isósceles com dois lados iguais ao raio da circunferência. Assim, você pode calcular o ângulo entre esses lados, porque como você tem 2n triângulos, e a circunferência toda tem 2.pi radianos, esse ângulo entre os lados iguais dos triângulos são todos iguais a 2.pi/2n, pois você dividiu a circunferência toda em 2n ângulos.
Agora você pode usar a fórmula da área do triângulo que usa dois lados e o seno entre eles para achar a área de um desses triângulos. Você tem dois lados iguais ao raio e o ângulo entre eles vale 2.pi/2n:
= r.r.sen(2.pi/2n)/2
= r2.sen(pi/n)/2
E você sabe que a área desse polígono é a soma de 2n vezes a área desse triângulo:
= 2n.r2.sen(pi/n)/2
= n.r2.sen(pi/n)
Para ficar parecido com o que usamos em s e S, vou chamar logo esse ângulo pi/n de “a”:
área I = n.r2.sen(pi/n)
área I = n.r2.(sen a)
Agora precisamos escrever isso em função de s e S. Aí é que vem a primeira complicação e que você precisa de um pouco de criatividade. Você tem que perceber que como você tem que sumir com o cosseno, você pode multiplicar s por S:
S.s = [n.r2.(sen a).(cos a)].[n.r2.(sen a)/(cos a)]
S.s = [n.r2.(sen a)].[n.r2.(sen a)]
S.s = [n.r2.(sen a)2].[n.r2]
S.s = n2.(r4).(sen a)2
Se tirar a raiz dos dois membros você chega na área I:
raiz(S.s) = n.r2.(sen a)
Então a área do polígono inscrito de 2n lados é igual a raiz(S.s).
Agora o polígono circunscrito de 2n lados também tem área semelhante ao circunscrito de n lados. Mas agora aquele ângulo que era alfa vai mudar. Agora o ângulo entre os dois lados dos 2n triângulos nesse polígono circunscrito de 2n lados é 2.pi/2n, ou seja pi/n que estamos chamando de “a” para facilitar. Só que se pegarmos um triângulo como fizemos para o polígono de n lados circunscrito (o triângulo da figura), onde tínhamos o ângulo “a” teremos agora a/2. E teremos que fazer a mesma coisa de novo para achar o lado desse polígono em função do raio e desse ângulo:
cos (a/2) = r/L
L.cos (a/2) = r
L = r/[cos (a/2)]
Agora podemos achar a área de um desses triângulos com dois lados iguais a r/[cos (a/2)] e o ângulo entre eles igual a “a” (2.pi/2n = pi/n):
= {r/[cos (a/2)]}.{r/[cos (a/2)]}.(sen a)/2
= r2.(sen a)/2.[cos (a/2)]2
E para melhorar a cara disso, vamos transformar cos (a/2) em cos a. Para isso usaremos a fórmula cos 2a = cos2 a – sen2 a:
cos 2a = cos2 a – sen2 a
cos a = cos2 (a/2) – sen2 (a/2)
cos a = cos2 (a/2) – [1 – cos2 (a/2)]
cos a = cos2 (a/2) – 1 + cos2 (a/2)
cos a = 2.cos2 (a/2) – 1
cos a + 1 = 2.cos2 (a/2)
(cos a + 1)/2 = cos2 (a/2)
cos2 (a/2) = (cos a + 1)/2
Como temos cos2 (a/2) na fórmula ficou mais fácil:
= r2.(sen a)/2.[cos (a/2)]2
= r2.(sen a)/2.[(cos a + 1)/2]
= r2.(sen a)/(cos a + 1)
E como essa é a área de um triângulo, para termos a área dos 2n triângulos, que é a área do polígono fazemos:
área II = 2n.r2.(sen a)/(cos a + 1)
Agora vem a pior coisa desse exercício, que é escrever isso em função de s e S. É depois de muita tentativa que você consegue fazer isso, não é só olhar e achar que vai fazer de cara, é difícil mesmo. Bom, vou tentar dizer como você poderia ir pensando pra fazer isso. Veja que no numerador você tem algo parecido com a área do polígono inscrito, que já vimos que era raiz(Ss):
área II = 2n.r2.(sen a)/(cos a + 1)
área II = 2.raiz(Ss)/(cos a + 1)
Agora você precisa ver se escreve o denominador também. Veja que se você tiver 1/(cos a) + 1 você pode chegar em algo parecido com o denominador:
1/(cos a) + 1 = (1 + cos a)/(cos a) (i)
Então se você olhar em S, você vê que tem um cos a no denominador também:
S = n.r2.(sen a)/(cos a)
E para ter 1/(cos a) + 1 você precisa ter outra expressão que tenha tudo o que S tem, menos o cos a no denominador. Mas n.r2.(sen a) é exatamente a raiz(Ss), então se somar os dois pode colocar n.r2.(sen a) em evidência:
S + raiz(Ss) = n.r2.(sen a)/(cos a) + n.r2.(sen a)
S + raiz(Ss) = n.r2.(sen a).[1/(cos a) + 1], aqui coloca i,
S + raiz(Ss) = n.r2.(sen a).(1 + cos a)/(cos a)
Mas desse jeito ainda não adianta, temos que sumir com n.r2.(sen a)/(cos a). Opa! Isso é igual a S! Então, temos que colocar um S multiplicando no numerador para cancelar, e aí ficamos com:
área II = 2.raiz(Ss)/(cos a + 1)
área II = 2.S.raiz(Ss)/[S + raiz(Ss)]
Respostas:
Polígono inscrito de 2n lados: raiz(S.s)
Polígono circunscrito de 2n lados: 2.S.raiz(Ss)/[S + raiz(Ss)]
Esse foi bem complicado. Espero que consiga entender tudo. Para você entender melhor aconselho ir escrevendo junto e colocando todas as passagens. Primeiro você poderia fazer a verificação da resposta, colocando os valores de S e s que encontramos nas áreas das respostas pra ver que dá realmente as áreas que encontramos.
